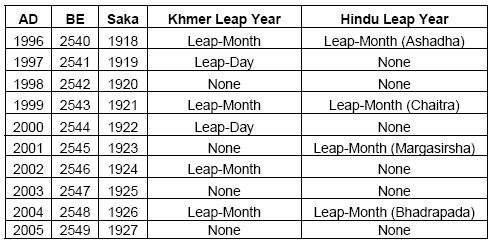
Table 1: List of years with leap-day and leap-month from the calendar printouts.
During my initial attempt to computerize the Khmer calendar calculation, I was not able to find any literature on how Khmer calendar works. So I attempt to collect data and try to find pattern to be able to generate the calendar dynamically.
Over the past seven years, I have collected Khmer calendar printouts. I thought that after collecting it for a few years, I would find a pattern and be able to formulate an algorithm to describe the calendar. I was far off the mark. As my understanding of the Khmer calendar system improved, I found it more mysterious. I talked to a few people who may have knowledge concerning the calendar but they implied that only the Horas know how the system works. Hora in this case refers to the astronomer not the fortuneteller.
Some Khmer calendar printouts distributed by the Khmer temple in CA, USA were not always correct. There is no clear source for an authoritative calendar except those that came from Cambodia. Sometimes calendars from different temples differ from each other. Therefore the religious holidays do not always coincide.
I collected my calendar resources in Long Beach, CA. I collected 16 calendar printouts that span 10 years. From these calendars, I attempted to find possible errors. After I was confident that my data was correct, I then mapped out each year. This gave me a mapping of the Khmer calendar dates from 1996 to 2005, including the interpolation I made for 2001 since I did not have the data. I determined which years were leap-month or leap-day years. I also included some comparisons to old Hindu lunisolar calendar leap years from Dershowitz and Reingold's book. This shows that the leap-months are not coincided with each other.
My goal is to find a pattern to identify which years are leap-month or leap-day years (year with extra month or extra day). Given that I have a rough idea that a leap-month year occurs every 2 to 3 years I thought that the data would be sufficient. Unfortunately I was not able to find any conclusive results.
The following table shows data I compiled from the calendar printouts.

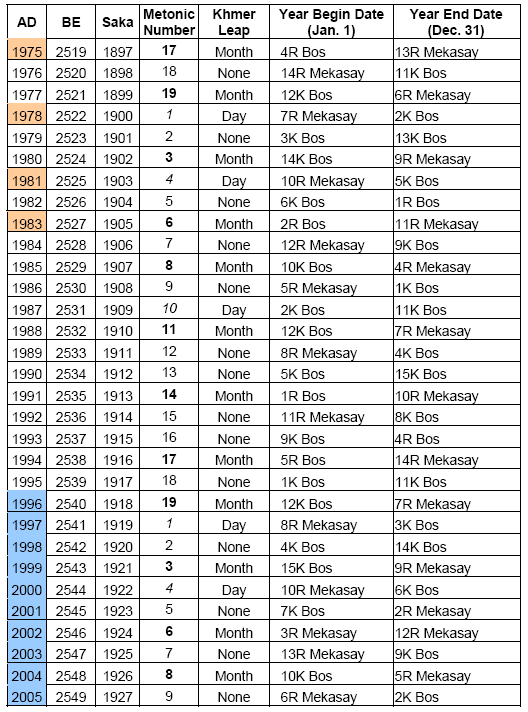
Finding more Khmer calendar printouts proved to be difficult. So my next approach is to try mapping out more years manually. In order to do this I need to have some certainty that the new data is correct. Fortunately, I found four dates that I know both from the Khmer calendar and the Gregorian calendar. These are birthdates in 1975, 1978, 1982, and 1983. Assuming that those dates were correct, I attempted to extrapolate the data from 1995 back to 1975.
As I further uncovered more background on lunisolar calendars, I found access to moon phase data. I also have some references to Khmer text indicating that Khmer New Year (usually April 13 or 14) must fall between certain Khmer months. This helped me to identify the leap years with the extra month. Also, the data on moon phases helped me to line up the Khmer dates more accurately.
With the resources above, I came up with the following criteria to extrapolate the data.
With those findings, I was able to map out 31 years (1975-2005) with a certain degree of confidence. Now, I can start to look for patterns.
In order to find the pattern we need to identify a cycle. I looked into a well-known cycle is called Metonic cycle. The Metonic cycle, discovered by a Greek astronomer Meton, synchronizes the solar and lunar year. He found that every 19 years the lunar and solar calendar coincided.
In fact, 235 lunar months (19 years) is 6,939.6884 days while 19 Tropical years is 6,939.6018 days. With 19 lunar years, we can have 7 leap months thus (19 years * 12 months/year) + 7 months is 235 months.
I found a reference claiming that Thai calendar follow the Metonic cycle but not as a rule. Since Khmer and Thai use the same system, I attempted to follow up on this. Since 6,939.60 days is not close to a whole day, the synchronization will be off by 0.6 days every 19 years. But if I attempt to use the Metonic cycle for Khmer calendar, these would be the calculations:
For Metonic 19-year cycle: 9 regular years * 354 days = 3,186 days 3 leap-day years * 355 days = 1,065 days 7 leap-month year * 384 days = 2,688 days Total: 6,939 daysSo for 19 years, it would sum up to 7 leap-months and 3 leap-days. This comes out to be 6,939.0 days. Thus this cycle generates about 0.688 day shorter than the lunar year every 19 years. So we can add an exception to compensate for the shortage. The cycle is shorter than the actual lunar cycle by about 0.6884 days every 19 years or 0.0362 days per year. An equivalent ratio, 17/494, which is 0.0344, is fairly close to use since 494 is a multiple of 19. By having 17 leap-day years every 494 years, we need to have 3 leap-day years every 4 Metonic cycles, or 18 leap-day years per 494 years. To get 17, we just subtract one leap-day year every 494 years.
By looking at the limited data, I can find the Metonic sequence (3, 6, 8, 11, 14, 17, and 19) by starting at the year 1978. This cycle seems to fit for leap-month years.
For leap-day years, I cannot use the Metonic cycle sequence number since it is already used for the leap-month year. But if I use Metonic cycle as a cycle, I should find that leap-day years repeat every cycle. The Metonic numbers for leap-day year are 1, 4, and 10. The cycle seems to match well with the existing data.
By extrapolating from the Metonic cycle described above, since 2009 AD is the leap-day year, we can add the first leap-day year on Metonic number 13.
| AD | BE | Saka | Metonic Number | Khmer Leap | Hindu Day on Jan. 1 |
Khmer Date on Jan. 1 | Khmer Date on Dec. 31 |
|---|---|---|---|---|---|---|---|
| 2005 | 2549 | 1897 | 9 | None | 21 | 6R Mekasay | 2K Bos |
| 2006 | 2550 | 1898 | 10 | Day | 2 | 3K Bos | 12K Bos |
| 2007 | 2551 | 1899 | 11 | Month | 13 | 13K Bos | 7R Mekasay |
| 2008 | 2552 | 1900 | 12 | None | 24 | 8R Mekasay | 5K Bos |
| 2009 | 2553 | 1901 | 13 | Day | 6 | 6K Bos | 15K Bos |
| 2010 | 2554 | 1902 | 14 | Month | 16 | 1R Bos | 10R Mekasay |
| 2011 | 2555 | 1903 | 15 | None | 27 | 11R Mekasay | 7K Bos |
| 2012 | 2556 | 1904 | 16 | None | 8 | 8K Bos | 4R Bos |
| 2013 | 2557 | 1905 | 17 | Month | 20 | 5R Bos | 14R Mekasay |
| 2014 | 2558 | 1906 | 18 | None | 1 | 1K Bos | 11K Bos |
| 2015 | 2559 | 1907 | 19 | Month | 11 | 12K Bos | 6R Mekasay |
| 2016 | 2560 | 1908 | 1 | Day | 22 | 7R Mekasay | 3K Bos |
| 2017 | 2561 | 1909 | 2 | None | 4 | 4K Bos | 14K Bos |
| 2018 | 2562 | 1910 | 3 | Month | 15 | 15K Bos | 9R Mekasay |
| 2019 | 2563 | 1911 | 4 | Day | 26 | 10R Mekasay | 5K Bos |
| 2020 | 2564 | 1912 | 5 | None | 6 | 6R Bos | 2R Bos |
Although I do not have enough concrete data to show multiple cycles of the Metonic cycles, the extrapolated data from 2006 to 2016 supports the use of Metonic cycle in Khmer calendar. In addition, running this method over 1,000 years, I found that the date still matches within the moon phase criteria. This approach can be a good estimate of how the calendar work.
There is no way to confirm that the extrapolated data is correct. So finding the Metonic number for leap-month year may not be correct. Those data can be adjusted to match or mismatch the cycle. The cycle only confirm that the synchronization between lunar and solar calendar is correct.
Even though the moon phase still coincide after running the algorithm over 1,000 year, it does not confirm that the actual calculation is the way that Khmer Horas does the calculation. For example, the leap month can be shifted by 1 years in the Metonic cycle and the moon phase would still within the acceptabble range.
In fact, with the new publication of the actual Horas' calculation, the Metonic cycle was not used. The next section will highlight the actual calculation.
| << Khmer Chhankitek | < Table of Content > | Calendar Algorithm >> |